반응형

1. 최단 경로 문제란?
: 가장 짧은 경로 내의 두 노드를 찾는 문제입니다. 변마다 가중치가 있는데, 가중치의 합이 최소가 되도록 경로를 찾아야 합니다.
2. 우선순위 큐
: 일반적인 큐(Queue)가 FIFO(First In First Out)구조였던 것에 비해, 우선순위 큐는 들어간 순서에 상관없이 우선순위가 높은 데이터가 먼저 나오는 자료구조입니다. 너비우선탐색(BFS)과 유사하며, 현재 가장 짧은 거리를 가진 노드 정보를 먼저 꺼내오는 방식으로, 최단 경로 문제를 푸는데 최적화 되어 있는 방법입니다.
저는 MinHeap 방식을 사용해 우선순위 큐를 구현할 것입니다.
* Heap :
https://geukggom.tistory.com/163
[C# 기초] #21. 힙(Heap)
1. 힙이란? : 완전 이진 트리(Complete Binary Tree)의 일종. 여러 값의 데이터들 중 최대값과 최소값을 빠르게 찾아낼 수 있는 자료구조입니다. (시간복잡도로 따지면 O(logn)이 걸림) * 힙의 특징 - 중복
geukggom.tistory.com
3. 다익스트라(Dijkstra) 알고리즘(우선순위 큐를 사용)
다음 그래프를 예시로 들어보겠습니다.
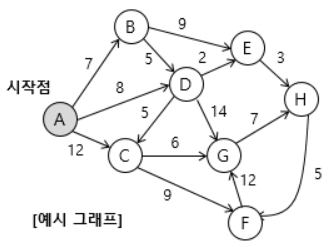
아래와 같이 엣지를 만든 후,
public class Edge : IComparer
{
public int distance;
public string vertex;
public Edge(int distance, string vertex)
{
this.distance = distance;
this.vertex = vertex;
}
public int Compare(object x, object y)
{
Edge _x = x as Edge;
Edge _y = y as Edge;
return _x.distance - _y.distance;
}
}
Hashtable로 graph를 구현해줍니다.
Hashtable graph = new Hashtable();
private void Start()
{
graph.Add("A", new Edge[] { new Edge(7,"B"), new Edge(8, "D"), new Edge(12, "C") });
graph.Add("B", new Edge[] { new Edge(5,"D"), new Edge(9, "E") });
graph.Add("C", new Edge[] { new Edge(6,"G"), new Edge(9, "F") });
graph.Add("D", new Edge[] { new Edge(2,"E"), new Edge(14, "G") });
graph.Add("E", new Edge[] { new Edge(3,"H") });
graph.Add("F", new Edge[] { new Edge(12,"G") });
graph.Add("G", new Edge[] { new Edge(7,"H") });
graph.Add("H", new Edge[] { new Edge(5,"F") });
}
MinHeap도 구현해줍니다.
public class MinHeap
{
public List<Edge> minHeap = new List<Edge>();
public bool addHeap(Edge data)
{
if(minHeap.Count == 0)
{
minHeap = new List<Edge>();
minHeap.Add(null); //0번 인덱스는 사용하지 않음(계산하기 편하게 하기 위해)
minHeap.Add(data); //1번 인덱스부터 데이터를 넣음.
}
else
{
minHeap.Add(data);
int parent_i, insert_i = minHeap.Count - 1; //추가
while (is_up(insert_i)) //insert_i를 부모노드와 크기 비교
{
parent_i = insert_i / 2;
swap(minHeap, insert_i, parent_i); //두 데이터 위치를 바꿈
insert_i = parent_i;
}
}
return true;
}
public void swap(List<Edge> a, int i1, int i2)
{
Edge temp = a[i1];
a[i1] = a[i2];
a[i2] = temp;
}
public Edge heapOut()
{
if (minHeap.Count == 0) return null;
Edge outData = minHeap[1]; //최소값을 가져옴
minHeap[1] = minHeap[minHeap.Count - 1]; //마지막 값을 가져옴
minHeap.RemoveAt(minHeap.Count - 1);
int idx = 1;
int i_left, i_right;
while (is_down(idx))
{
i_left = idx * 2;
i_right = idx * 2 + 1;
if (i_right >= minHeap.Count && minHeap[idx].distance > minHeap[i_left].distance)
{
swap(minHeap, idx, i_left);
idx = i_left;
}
else if (i_right < minHeap.Count)
{
if (minHeap[i_left].distance < minHeap[i_right].distance)
{
swap(minHeap, idx, i_left);
idx = i_left;
}
else
{
swap(minHeap, idx, i_right);
idx = i_right;
}
}
}
return outData;
}
}
이제 다익스트라 알고리즘을 만들어줍니다.
1) 각 노드마다 인접한 간선들을 확인
2) 미니힙에 노드, 거리 정보를 넣고 pop(꺼내오고 삭제)
public Hashtable dijkstraFunc(Hashtable graph, string start)
{
Edge edgeNode, adjNode;
int currentDistance, weight, distance;
string currentNode, adjacent;
Edge[] nodeList;
Hashtable shortDistance = new Hashtable();
ICollection keyColl = graph.Keys;
foreach (string a in keyColl) //graph 안의 key값을 모두 옮기고, 최대 거리값을 넣어줌
{
shortDistance.Add(a, int.MaxValue);
}
shortDistance[start] = 0;
MinHeap prioQueue = new MinHeap(); //미니힙 생성
prioQueue.addHeap(new Edge((int)shortDistance[start], start));
int count=0;
while (prioQueue.minHeap.Count > 1 && count<150)
{
count++;
edgeNode = prioQueue.heapOut(); //미니힙에 노드, 거리 정보를 넣고 pop(꺼내오고 삭제)
currentDistance = edgeNode.distance;
currentNode = edgeNode.vertex;
if ((int)shortDistance[currentNode] < currentDistance) continue;
nodeList = (Edge[])graph[currentNode]; //인접한 간선 확인
for (int i = 0; i < nodeList.Length; i++)
{
adjNode = nodeList[i];
adjacent = adjNode.vertex;
weight = adjNode.distance;
distance = currentDistance + weight;
if (distance < (int)shortDistance[adjacent]) //거리가 더 짧을 때만 업데이트
{
shortDistance[adjacent] = distance;
prioQueue.addHeap(new Edge(distance, adjacent));
}
}
}
foreach (string a in keyColl)
{
Debug.Log(a+"?"+ shortDistance[a]);
}
return shortDistance;
}
반응형
'[Computer Science] > [알고리즘]' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리 (feat.프림 알고리즘) (0) | 2022.02.14 |
|---|---|
| [알고리즘] 최소 신장 트리 (feat.크루스칼 알고리즘) (0) | 2022.02.12 |
| [알고리즘] 탐욕 알고리즘(Greedy algorithm) (0) | 2022.02.09 |
| [알고리즘] 탐색 알고리즘(feat. 순차탐색, 이진탐색) (0) | 2022.02.08 |
| [알고리즘] 퀵정렬(Quick sort) (0) | 2022.02.07 |